요약
| 정렬 | Best | Average | Worst | In-place | Stable |
|---|---|---|---|---|---|
| 선택 | O | X | |||
| 삽입 | O | O | |||
| 버블 | O | O | |||
| 퀵 | O | X | |||
| 병합 | X | O | |||
| 힙 | O | X | |||
| 기수 | X | O |
1. 정렬(Sort)
-
정렬: 레코드(키+필드)를 키의 순서대로 재배열하는 작업
- 모든 경우에 최적인 정렬 알고리즘은 없음
- 데이터의 형식, 수, 크기에 따라 적합한 방법 선택
-
레코드(record): 하나의 데이터 단위
- 키(key): 정렬 기준이 되는 필드
- 필드(field): 레코드를 구성하는 각각의 정보 항목
1.1. 정렬 관련 용어
-
우수한 정렬 알고리즘의 성질
- 제자리 정렬(in-place): 입력 배열 외에 추가 메모리를 거의 사용하지 않는 정렬
- 안정 정렬(stable): 같은 키 값을 가진 레코드들의 상대적 순서가 유지되는 정렬
-
모든 데이터가 메모리에 올라오는가?
- 내부 정렬: 모든 레코드가 메인 메모리에 올라와 있는 정렬
- 외부 정렬: 대부분의 데이터가 외부 기억 장치에 있고, 일부만 메모리에 올라와 있는 대규모 정렬
-
가정: 본 장에서는 정수형 키를 가진 1차원 배열을 오름차순으로 정렬하는 경우를 다룹니다.
2. 비교 정렬(comparison)
2.1.
(1) 선택 정렬(selection)
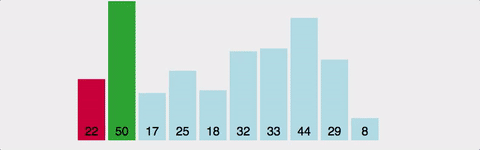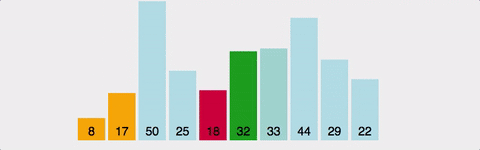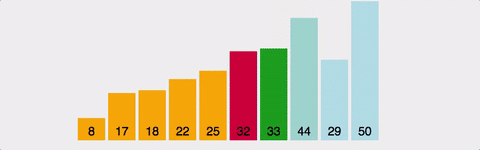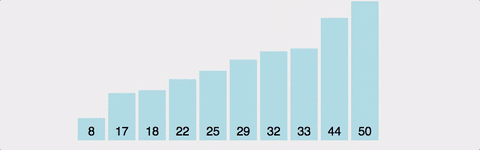
- step: 1 to n-1
- comp: (step에 따라, 항상) n-1 to 1
- swap: O (제자리 정렬)
void selection_sort(int arr[], int n) {
for (int i = 0; i < n-1; i++) {
int min = i;
for (int j = i+1; j < n; j++)
if (arr[j] < arr[min]) min = j;
swap(&arr[i], &arr[min]);
}
}(2) 삽입 정렬(insertion)
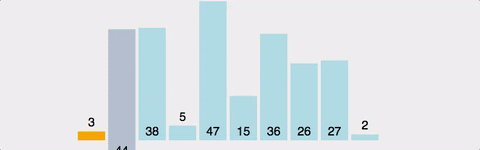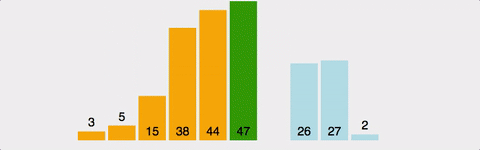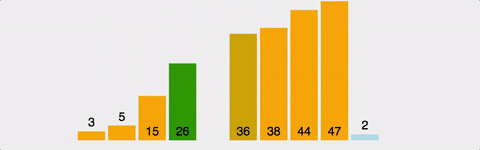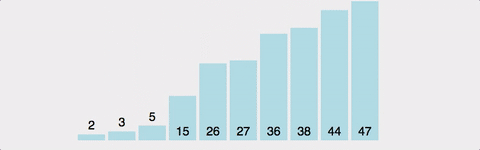
- step: 2 to n
- min_comp: 1
- max_comp: (step에 따라) 1 to (n-1)
- swap: O (제자리 정렬)
void insertion_sort(int arr[], int n) {
for (int i = 1; i < n; i++) {
int j = i;
while (j > 0 && arr[j-1] > arr[j]) {
swap(&arr[j], &arr[j-1]);
j--;
}
}
}(3) 버블 정렬(bubble)
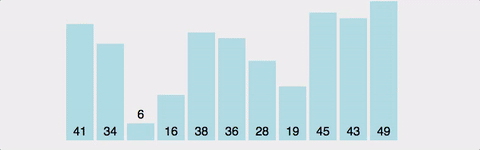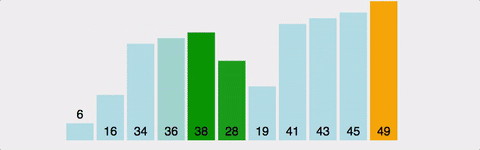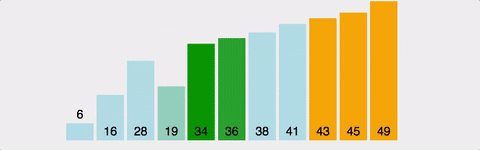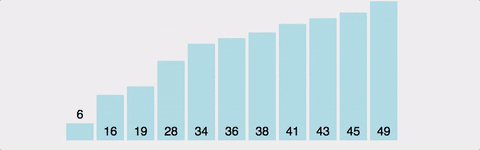
- step: 1 to n-1
- min_comp: 1
- max_comp: (step에 따라) (n-1) to 1
- swap: O (제자리 정렬)
void bubble_sort(int arr[], int n) {
for (int i = 0; i < n-1; i++)
for (int j = 0; j < n-1-i; j++)
if (arr[j] > arr[j+1])
swap(&arr[j], &arr[j+1]);
}2.2.
(1) 병합 정렬(merge)
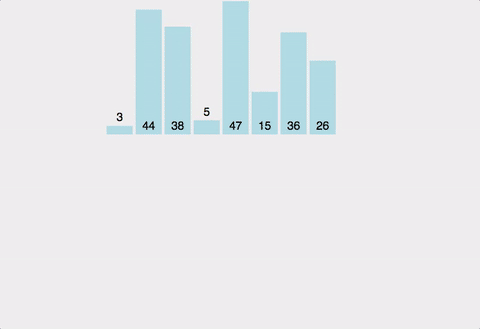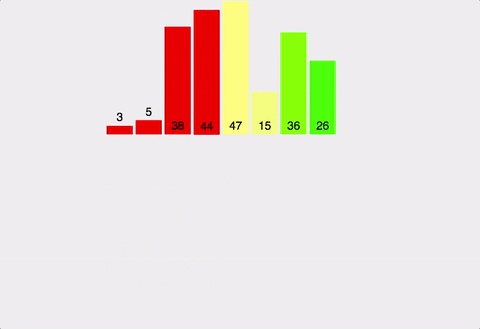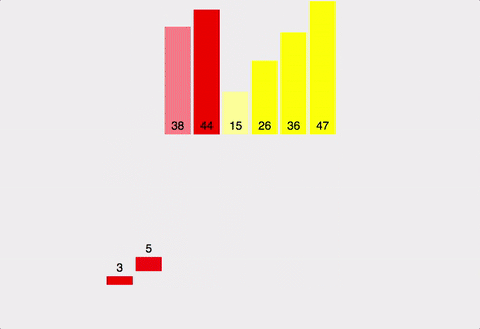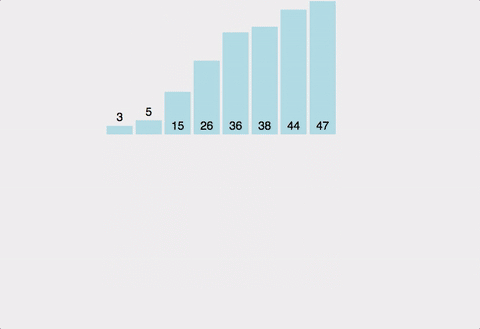
- 분할 정복(divide and conquer)
- 분할: 분할 비용
- 정복/병합: 각 recursion depth()마다 병합 비용
- 시간 복잡도:
- 공간 복잡도: 병합 시 정렬된 배열을 따로 생성하는 비제자리 정렬
void merge_sort(int arr[], int low, int high) {
if (low < high) {
int mid = (low+high)/2;
merge_sort(arr, low, mid);
merge_sort(arr, mid+1, high);
merge(arr, low, mid, high);
}
}
void merge(int arr[], int l, int m, int r) {
int n1 = m-l+1, n2 = r-m;
int L[100], R[100]; // subarray L, R
for (int i = 0; i < n1; i++) L[i] = arr[l + i];
for (int i = 0; i < n2; i++) R[i] = arr[m + 1 + i];
int i = 0, j = 0, k = l;
while (i < n1 && j < n2)
arr[k++] = (L[i] <= R[j]) ? L[i++] : R[j++]; // 조건?참:거짓
while (i < n1) arr[k++] = L[i++]; // 남은 배열 소진
while (j < n2) arr[k++] = R[j++]; // 남은 배열 소진
}(2) 퀵 정렬(quick)
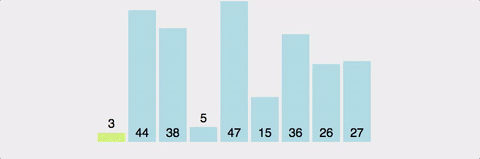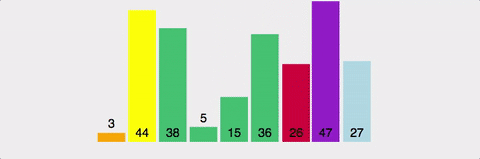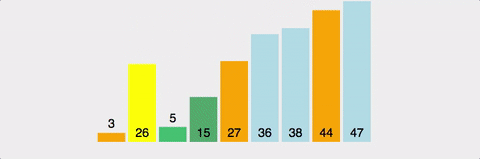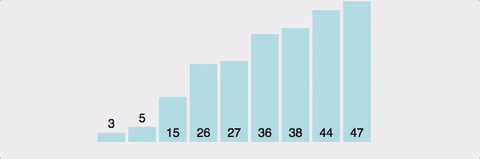
-
comp: n
-
recursion depth: (best) ~ (worst: pivot이 min/max일 때)
- median of three: pivot을 왼쪽, 가운데, 오른쪽 중 중간값으로 사용
-
swap: O (제자리 정렬)
-
불안정 정렬
-
알고리즘
- 좌우에서 포인터를 이동시키며, 피벗보다 큰 값·작은 값을 교환
- 두 포인터가 교차하면 분할 완료
void quick_sort(int arr[], int low, int high) {
if (low < high) {
int pivot = partition(arr, low, high);
quick_sort(arr, low, pivot-1);
quick_sort(arr, pivot+1, high);
}
}
int partition(int arr[], int low, int high) {
int pivot = arr[high];
int i = low;
for (int j = low; j < high; j++) {
if (arr[j] < pivot) swap(&arr[i++], &arr[j]);
}
swap(&arr[i], &arr[high]);
return i;
}- 퀵 정렬 라이브러리 함수
- qsort(): C 기본 라이브러리 제공, 함수 포인터로 비교 함수를 전달하며 내부적으로 퀵 정렬 계열 알고리즘을 사용
(3) 힙 정렬(heap)
-
힙 자료구조를 이용하여 정렬하는 방식
- 최대 힙(max heap): 루트가 최댓값이 되도록 구성
- 시간 복잡도: 모든 경우
- 공간 복잡도: (제자리 정렬)
- 불안정 정렬
-
작동 방식
- 배열을 최대 힙으로 구성 (build heap)
- 루트(최댓값)와 마지막 원소 교환 후 힙 크기 줄임
- 다시 힙 재정렬(heapify) 반복
3. 비비교 정렬(non-comparison)
3.1. 기수 정렬(radix)
-
비교 기반 정렬의 한계를 넘어, 키의 자리수(digit)에 따라 “버킷(bucket)”에 분배한 뒤 다시 모으는 과정을 반복하는 방식입니다.
-
LSD(Least Significant Digit) 방식: 가장 낮은 자리수부터 높은 자리수 순으로 안정적 정렬
-
MSD(Most Significant Digit) 방식: 가장 높은 자리수부터 낮은 자리수 순으로 분할 정복
for (d = 0; d < max_digits; d++) {
// 각 원소를 d번째 자리수 값에 따라 10개의 큐에 분배
distribute(a, buckets, d);
// 버킷 순서대로 a[]에 다시 복귀
collect(a, buckets);
}- 시간 복잡도: O(dn), 실제 d(자릿수)가 작아 선형 시간에 가까움
- 특징
- 버킷 방식으로 안정성을 만족
- 버킷(추가 큐)로 인한 비제자리 정렬
- 한정된 키 타입(동일 길이 숫자, 단순 문자 등)에만 적용 가능
4. 함수 포인터
- 비교 기준을 함수 포인터로 전달하여, 다양한 기준으로 동일한 정렬 알고리즘을 적용할 수 있는 기법입니다.
- Lab 9.1: 2차원 좌표 구조체에 대해 x-좌표, y-좌표, 거리 기준 등 다양한 비교 함수를 구현하고, 삽입 정렬이나 qsort()에 전달하여 정렬
int x_ascend(Element a, Element b) { // x 오름차순
return (b.x - a.x);
}
int y_descend(Element a, Element b) { // y 내림차순
return (a.y - b.y);
}
int z_ascend(Element a, Element b) { // 크기의 오름차순
return ((b.x * b.x + b.y * b.y) - (a.x * a.x + a.y * a.y));
}
void insertion_sort_fn(Element A[], int n, int(*f)(Element, Element)) {
for (int i = 1; i < n; i++) {
Element key = A[i];
int j;
for (j = i - 1; j >= 0; j--) {
if (f(A[j], key) < 0) A[j + 1] = A[j];
else break;
}
A[j + 1] = key;
}
}
void main() {
Element list[9] = {
{6,6}, {7,4}, {2,3}, {1,5}, {5,2}, {3,3}, {9,4}, {1,8}, {5,3}
};
insertion_sort_fn(list, 9, x_ascend);
insertion_sort_fn(list, 9, y_descend);
insertion_sort_fn(list, 9, z_ascend);
}